CALCULO VECTORIAL
-CAPITULO I
1.1 GEOMETRÍA ANALÍTICA EN EL ESPACIO:
1.1.1 En dos dimensiones (F(x,y)=0)
El estudio de la geometría analítica en el espacio primero necesitara de los conocimientos básicos de una geometría en el plano.
La geometría en el plano trabaja tan solo con dos variables que son x ^ y, en la cual una depende de la otra ya sea "x" o "y".
y=f(x) x=f(y)
En el plano si una variable esta en función de la otra generara una curva (figura 1).
 |
Figura 1:Circunferencia con centro (h,k), se genera con la ecuación  (http://www.eva.com.mx/sia/materias/mat_056/podi/U9_liga2.html) |
En la ecuación de la circunferencia la función se la puede hacer explicita despejando cualquiera de las dos variables.
Sistema de funciones implicitas: A la intersección de dos ó mas funciones se la denomina sistema de funciones implícitas, si el sistema tiene solución, significa que las soluciones corresponden a los puntos de intersección de las curvas en el plano (figura 2).
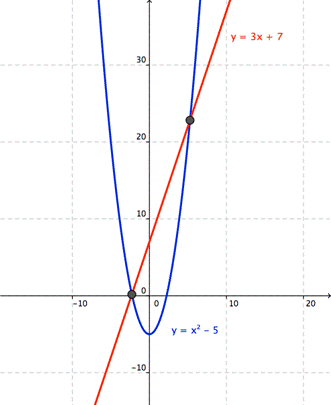 |
| Figura 2: intersección entre dos funciones, los puntos comunes de las dos funciones serán la solución del sistema. (http://www.montereyinstitute.org/courses/Algebra1/COURSE_TEXT_ RESOURCE/U10_L2_T2_text_container_es.html |
Ya con los conocimientos básicos en el plano ahora se puede hablar sobre gráficas en tres dimensiones o también llamadas en el espacio.
En el espacio se trabaja con tres variables x, y ^ z, en donde una variable esta en funcion de las otras dos ya sea "x", "y" ó "z".
A la ecuación de las superficie esférica se la puede hacer explicita despejando cualquiera de las tres variables y así una quedaría en función de las otras dos.
x=f(y,z) y=f(x,z) z=f(x,y)
En el espacio si una variable esta en función de la otra ó otras dos se genera una superficie (figura 3).
 |
| x2 + y2 + z2 = R2 Figura 3:Representación en el espacio de la superficie esférica. (http://es.wikipedia.org/wiki/Esfera) |
NOTA: Por conveniencia se tomara al eje vertical como "z", al eje horizontal como "y" y al eje inclinado como "x".
GENERATRIZ: Es una linea que a causa de su movimiento genera una figura geométrica, en este caso generaría la superficie.
No siempre participan las 3 variables en una función , tal que la variable dependiente estaría en función tan solo de una y no de las dos, si sucede este caso se dice que la generatriz es paralela al eje de la variable no participante. (figura 4)
 |
| Figura 4a: Plano con generatriz paralela al eje x, es decir F(y,z)=0 con x=0 |
 |
| Figura 4b: Plano con generatriz paralela al eje y, es decir F(x,z)=0 con y=0 |
 |
| Figura 4c: Plano con generatriz paralela al eje z, es decir F(x,y)=0 con z=0 |
Figura 4: Los tres casos distintos en donde participan solo dos variables y la tercera es cero.
NOTA: Si tan solo participara una variable la generatriz seria paralela a los dos ejes restantes, teniendo los siguientes casos:
- F(x)=0 y y=0, z=0 con generatriz paralela a los ejes y ^ z.
- F(y)=0 y x=0, z=0 con generatriz paralela a los ejes x ^ z.
- F(z)=0 y y=0, x=0 con generatriz paralela a los ejes y ^ x.
Sistema de funciones implicitas: A la intersección de dos ó mas funciones se la denomina sistema de funciones implícitas,ahora, si es en el espacio dependería del número de funciones que participaran en el sistema.
a) Si tan solo participasen dos funciones su intersección generaría una curva. (figura 5)
a) Si tan solo participasen dos funciones su intersección generaría una curva. (figura 5)


Figura 5: Sistema de dos ecuaciones en el espacio,cuya intersección genera una circunferencia.
b) Si participasen tres o mas funciones generarían puntos en común entre las funciones participantes.(figura 6)
 |
| Figura 6: Intersección de tres planos que en este caso generaria tan solo un punto en común entre los tres planos. (http://temasmatematicos.uniandes.edu.co/Seminario/paginas/Seminario_03/) |
..........................................................................................................................................................
1.2 LA RECTA EN R3.
1.2.1 ecuación de la recta:
En el espacio una recta viene determinada por un punto A (x0,y0,z0) y un vector u=(l,m,n), cuya dirección es la recta que pasa por los puntos A y P (x,y,z). llamando a u vector director que irá desde el punto A hasta el punto P. La distancia que separa A de P sera "t veces" el vector u.(figura 7)
1.2.1 ecuación de la recta:
En el espacio una recta viene determinada por un punto A (x0,y0,z0) y un vector u=(l,m,n), cuya dirección es la recta que pasa por los puntos A y P (x,y,z). llamando a u vector director que irá desde el punto A hasta el punto P. La distancia que separa A de P sera "t veces" el vector u.(figura 7)
 |
| Figura 7: Gráfica tridimensional de una recta. (http://www.sc.ehu.es/sbweb/energias-renovables/MATLAB/simbolico/geometria/geometria.html) |
Hablando de la recta, hay tres maneras distintas de representarla las cuales son:
- Ecuación vectorial.
- Ecuaciones paramétricas.
- Ecuaciones canónicas, cartesianas o simétricas.
REPRESENTACIÓN: En futuros ejercicios que nos pida la ecuación de la recta se necesita los siguientes datos.
1.- CASO 1
Se necesitaran de los datos: u=(a,b,c)
A=(ro) donde ro =(xo,yo,zo)
La ecuación vectorial es:
r = r0 + tu
Las ecuaciones parametricas serán:
r = r0 + tu
Las ecuaciones parametricas serán:
_________________________________________
Las ecuaciones canónicas serán:
_________________________
2.- CASO 2
En este caso se necesitaran como datos dos puntos pertenecientes a la recta.
M1(ro) donde ro=(xo,yo,,zo)
M2(r1) donde r1=(x1,y1,z1)
En este caso se necesitaran como datos dos puntos pertenecientes a la recta.
M1(ro) donde ro=(xo,yo,,zo)
M2(r1) donde r1=(x1,y1,z1)
La ecuación vectorial sera:
r = r1 + t(r1-ro)
r = r1 + t(r1-ro)
1.2.2 Distancia de un punto a una recta:
Para encontrar la distancia entre un punto y la recta se necesitan los siguientes datos:
-r = r0 + ta
- M1(r1)
Para encontrar la distancia entre un punto y la recta se necesitan los siguientes datos:
-r = r0 + ta
- M1(r1)
 |
| Figura 8: Representación gráfica de la distancia entre un punto y la recta. |
1.2.3 Distancia entre dos rectas
Para encontrar la distancia entre dos rectas se necesitan los siguientes datos:
-r = r01 + ta
-r = r02 + ta
 |
| Figura 9: Representación gráfica de la distancia entre dos rectas. |
_________________________
1.2.4 Interpretación del producto mixto
En el caso de la distancia entre dos rectas se aplico el producto mixto, es decir: A.BXC
Geometricamente este producto mixto es el volumen de un paralelepípedo.(figura 10).
| Figura 10: El volumen del paralelepípedo vendría dado por el producto mixto entre los vectores [U,V,W] (http://www.tmoya.es/geometria/espacio/producto.html) |
V=U.VxW
------------------------------------------------------------------------------------
1.3 EL PLANO EN R3
Así como la recta viene determinada por " un punto A (x0,y0,z0) y un vector u=(l,m,n), cuya dirección es la recta que pasa por los puntos A y P (x,y,z)".
El plano dependería de como mínimo un punto y un vector normal n ó tres puntos.
Hay cuatro tipos de ecuaciones diferentes para representar matemáticamente a un plano siendo estas:
- Ecuación vectorial del plano.
- Ecuación general del plano.
- Ecuación segmentaria del plano.
- Ecuación normal del plano.
1.3.1 Ecuación vectorial del plano.
La representación por esta esta ecuación necesita de los siguientes datos:
P(r0) donde r0=(x0,y0,z0)
n=(A,B,C)
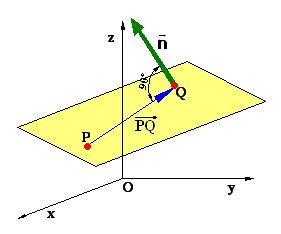 |
| figura 11: Representación gráfica de un plano en el espacio cuya ecuación depende de un punto y el vector normal. (http://www.aulafacil.com/cursos/l10897/ciencia/matematicas/planos-en-el-espacio/ecuacion-normal) |
La ecuación vectorial del plano es:
(r-r0).n=0
1.3.2 Ecuación general del plano.
Esta ecuación se deriva de la ecuación vectorial reemplazando r por (x,y,z); r0 por (x0,y0,z0) y n por (A,B,C), realizando operaciones matematicas le llega a la ecuación:
Ax+By+Cz+D=0
* D= -(Ax0+By0+Cz0) y es un número debido a que todos estos valores son numéricos.
*Como se menciono anteriormente si A,B ó C es cero la gráfica tendera una generatriz paralela a su respectivo eje, lo mismo se dijo si dos variables se hacen cero la generatriz será paralela a sus respectivos ejes.
1.3.3 Ecuación segmentaria del plano.
Un plano con sus tres componentes x,y, ^ z, corta obligatoriamente los tres ejes en un punto especifico, estos puntos específicos son:P1(a,0,0)
P2(0,b,0)
P3(0,0,c)
Para llegar a determinar los valores de a,b y c se divide a la ecuación general del plano para D
Entonces quedaría la expresión:
Donde: a= -D/A; b=-D/B ; c=-C/D
 |
| Figura 12: Representación gráfica de la ecuación segmentaria del plano, en este se detallan los cortes en x, y ^ z. (http://www.vadenumeros.es/segundo/ecuaciones-de-un-plano.htm) |
1.3.4 Ecuación normal del plano:
La ecuación normal del plano se caracteriza por trabajar con el unitario del vector normales decir con sus ángulos directores,entonces los datos necesarios seran:
 |
| Figura 13: Representación gráfica de la ecuación normal. |
1.3.4.1 Normalización de la ecuación general del plano:
Para normalizar la ecuación del plano se hace uso de un factor normalizante:
Que multiplicara a compenente de la ecuación, es decir:
El factor normalizante es:

NOTA: El factor normalizante debe ser de signo contrario a D
1.3.5 Distancia entre un punto y el plano:
La distancia entre un punto y el plano debe representar su distancia perpendicular (figura 14).
 |
| Figura 14: Representación gráfica de la distancia entre un punto y el plano. "Dicha distancia es perpendicular al plano". |
La distancia viene determinada por:
1.3.6 Plano determinado por tres puntos
Ya habia mencionado que para determinar la ecuación del plano se necesita o bien un punto y el vector normal o tres puntos (figura 15), ya estudiado el primer caso ahora se determinara la ecuación por tres puntos:
Datos:
- P1(r1)
- P2(r2)
- P3(r3)
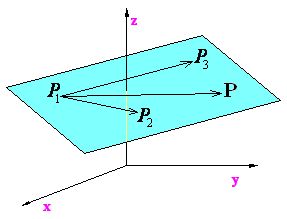 |
| Figura 15: Plano determinado por 3 puntos. (http://www.aulafacil.com/cursos/l10895/ciencia/matematicas /planos-en-el-espacio/ecuacion-del-plano-que-pasa-por-tres-puntos) |
El plano viene determinado por la siguiente ecuación:
(r-r1).(r2-r1)x(r3-r1)=n
NOTA: Si el producto mixto da como resultado 0, entonces se dice que los tres vectores son coplanares.
1.3.7 Recta determinada por dos planos.
Se menciono anteriormente que en un sistema de ecuaciónes de dos funciones se generaban curvas, pues bien en la intersección de dos planos se genera una recta (figura 16), para representar de manera matemática a esta recta se tiene:
Datos:
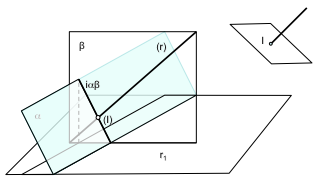 |
| Figura 16: Recta formada por dos planos. (http://piziadas.com/2012/04/sistemas-de-representacion-incidencia -intersecciones-geometria-descriptiva.html) |
Los vectores normales serán:
Haciendo un productos cruz entre estos dos vectores se obtiene un vector perpendicular a dichos vectores y este sera el vector director de la recta que se quiere calcular, obteniendo:
Luego se toma un punto de referencia con respecto a los planos esto se logra haciendo 0 a cualquiera de las variables en las dos ecuaciones, obteniendo un sistema de dos ecuaciones con dos incógnitas:
PARA X=0
Para determinar la ecuación de una recta se necesita el vector director y punto entonces las ecuaciones canónicas de la recta serán:
1.3.8 Ecuación de un haz de planos.
Se denomina haz de planos a la intersección de infinitos planos que coinciden en una misma recta (figura 17).
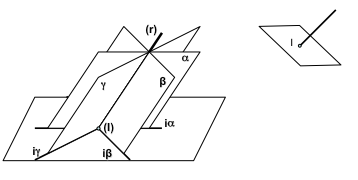 |
| Figura 17: Intersección de planos que coinciden en una misma recta. (http://piziadas.com/wp-content/uploads/2012/04/Intersecci%C3%B3n-de-recta-y-plano.png) |
Datos:
Multiplicando al plano 1 por alfa, al plano 2 por beta y sumando las dos ecuaciones se tiene:
Dividiendo toda la ecuación para alfa se obtiene:
Haciendo un cambio de variable y agrupando se llega a la ecuación requerida:
 |
| Ecuación del haz de planos. |
El vector normal de esta haz de planos seria:
1.3.8 Ecuación de la superficie esférica.
 |
| figura 18: superficie esferica. http://www.monografias.com/trabajos94/superficies-cuadricas-2/superficies-cuadricas-2.shtml |
Son todas aquellas que se representan por :
Se denominan también cuadráticas.
Escogiendo sistemas coordenados adecuados se puede simplificar su ecuación.
Para realizar su análisis y respectivamente su gráfica se realizan los siguientes pasos:
- Intersección con los ejes coordenados.
- Intersección con los planos coordenados.
- Intersección con planos paralelos a los planos coordenados.
- Trazado del bosquejo de la superficie de estudio.
Tipos de superficie.
a.- Elipsoide:
Ecuación:

representación tridimensional
 |
| Figura 19: Elipsoide. http://www.matematicasypoesia.com.es/matematicas/SupSegOrden.htm |
b.- Hiperboloide de una hoja:
Ecuación

Representación tridimensional:
 |
| Figura 20: Hiperboloide de una hoja. http://www.matematicasypoesia.com.es/matematicas/SupSegOrden.htm |
c.- Hiperboloide de dos hojas:
Ecuación:

Representación tridimensional:
 |
| Figura 21: Hiperboloide de dos hojas. http://www.matematicasypoesia.com.es/matematicas/SupSegOrden.htm |
d._ Paraboloide elíptico:
Ecuación:

Representación tridimensional:
 |
| Figura 22: Paraboloide eliptico: http://www.matematicasypoesia.com.es/matematicas/SupSegOrden.htm |
e.- Paraboloide hiperbólico:
Ecuación:

Representación tridimensional:
 |
| Figura 23:Paraboloide hiperbólico. http://www.matematicasypoesia.com.es/matematicas/SupSegOrden.htm |
f.- Conos:
Ecuación:

Representación tridimensional
 |
| figura 24: conos. http://www.matematicasypoesia.com.es/matematicas/SupSegOrden.htm |
Ecuación:

Representación Tridimensional:
 |
| Figura 25: Cilindro. http://www.matematicasypoesia.com.es/matematicas/SupSegOrden.htm |














No hay comentarios:
Publicar un comentario